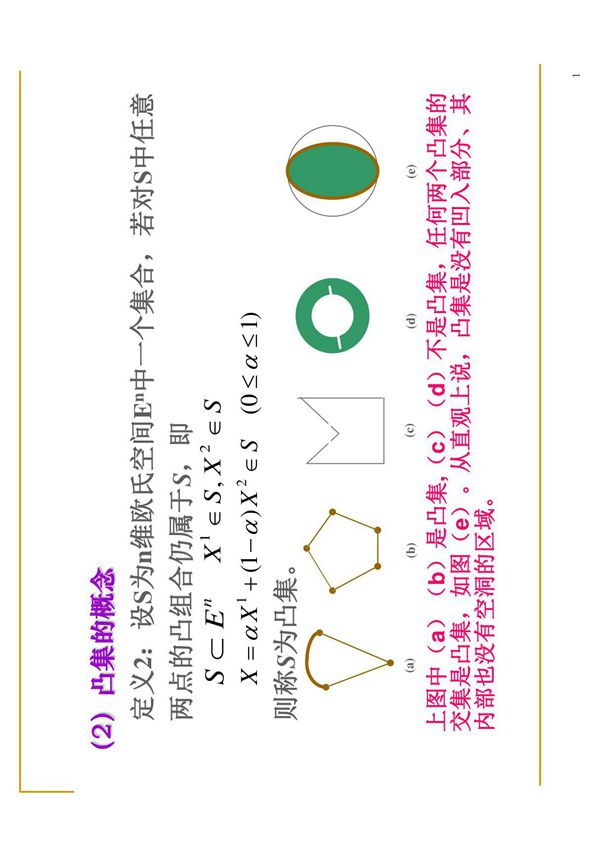
凸集是凸分析中的一个基本概念,广泛应用于优化理论、经济学和工程等领域。简单来说,如果一个集合中的任意两点之间的连线仍然完全包含在该集合内,那么这个集合就称为凸集。具体而言,设集合(Csubseteqmathbb{R}^n),若对于任意(x,yinC)和任意(thetain[0,1]),都有(thetax+(1-theta)yinC),则称(C)为凸集。凸集的性质在优化问题中尤为重要,因为许多优化算法依赖于目标函数和约束条件的凸性来保证全局最优解的存在性和唯一性。本节将详细介绍凸集的定义、基本性质以及相关定理,为后续学习凸优化奠定基础。