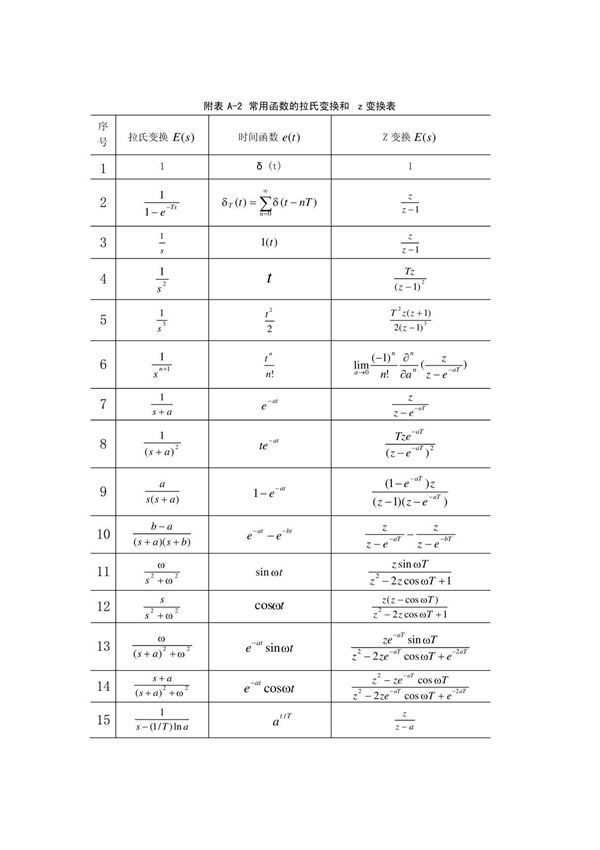
Z变换是一种在离散时间信号处理和系统分析中广泛使用的数学工具,它将离散时间信号从时域转换到复频域。Z变换在数字信号处理、控制系统和通信系统等领域有重要应用。以下是一些常见的Z变换及其简介:1.单位阶跃序列的Z变换:单位阶跃序列u[n]的Z变换为1/(1-z⁻¹),其中|z|>1。它表示离散时间中的阶跃信号,常用于分析系统的稳态响应。2.单位脉冲序列的Z变换:单位脉冲序列δ[n]的Z变换为1。这是最简单的Z变换,表示离散时间中的冲激信号,常用于系统建模和特性分析。3.指数序列的Z变换:指数序列aⁿu[n]的Z变换为1/(1-az⁻¹),其中|z|>|a|。这种变换在分析衰减或增长信号时非常有用。4.正弦序列的Z变换:正弦序列sin(ωn)u[n]的Z变换为(z⁻¹sinω)/(1-2z⁻¹cosω+z⁻²)。它用于分析离散时间系统中的振荡行为。5.余弦序列的Z变换:余弦序列cos(ωn)u[n]的Z变换为(1-z⁻¹cosω)/(1-2z⁻¹cosω+z⁻²)。与正弦序列类似,它用于分析振荡系统。6.斜变序列的Z变换:斜变序列nu[n]的Z变换为z⁻¹/(1-z⁻¹)²。这种变换在分析随时间线性变化的信号时非常有用。Z变换的这些基本形式为分析和设计离散时间系统提供了基础工具,通过它们可以求解差分方程、分析系统稳定性和频率响应等。