处处连续而处处不可导函数一例

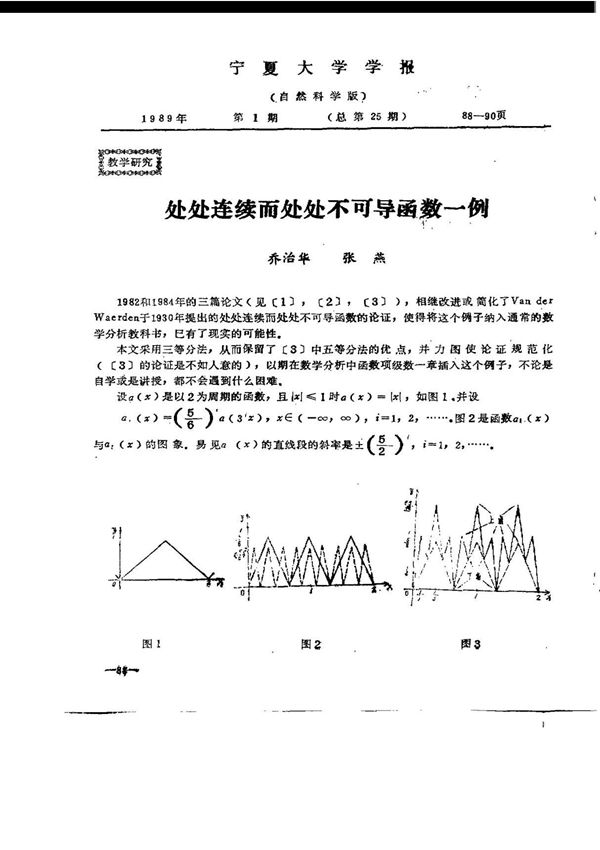
处处连续而处处不可导的函数是数学分析中一类特殊的函数，它们在每一点都连续，但在任何点都没有导数。这类函数打破了人们对于连续函数“光滑性”的直观想象，展示了连续性并不必然导致可微性。一个经典的例子是魏尔斯特拉斯函数（Weierstrassfunction），其定义为：f(x)=Σ_{n=0}^∞a^ncos(b^nπx)，其中01+(3π/2)。该函数在实数范围内处处连续，但由于其无限振荡的性质，在任何点都无法定义有限的导数。魏尔斯特拉斯函数的构造揭示了连续性与可微性之间的深刻差异，对19世纪的数学分析发展产生了重要影响。