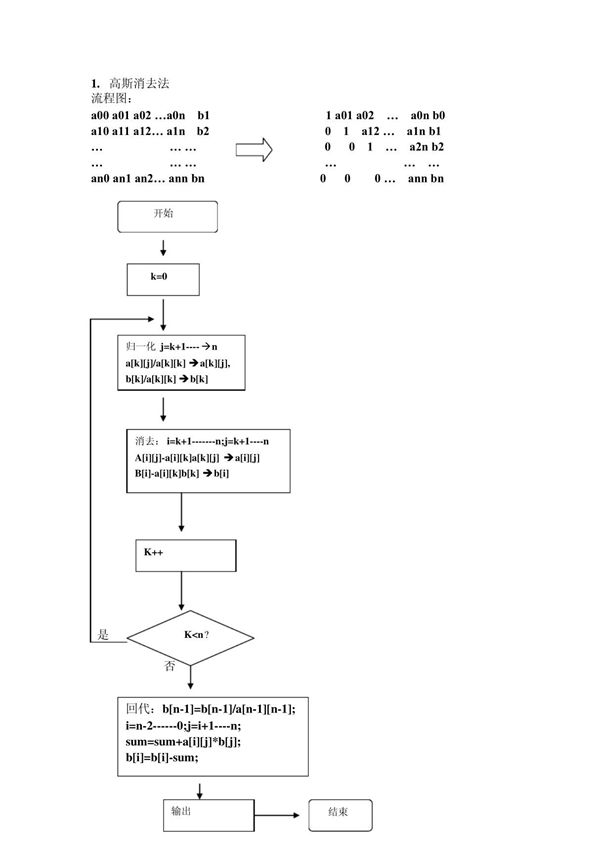
高斯消去法是一种用于解线性方程组的直接方法。它通过一系列初等行变换将系数矩阵转化为上三角矩阵，然后通过回代求解未知数。该方法分为两个主要步骤：消元过程和回代过程。消元过程通过行变换将矩阵化为上三角形式，回代过程则从最后一行开始逐步求解各个未知数。高斯消去法适用于任何非奇异矩阵，是数值线性代数中最基础且广泛应用的算法之一。