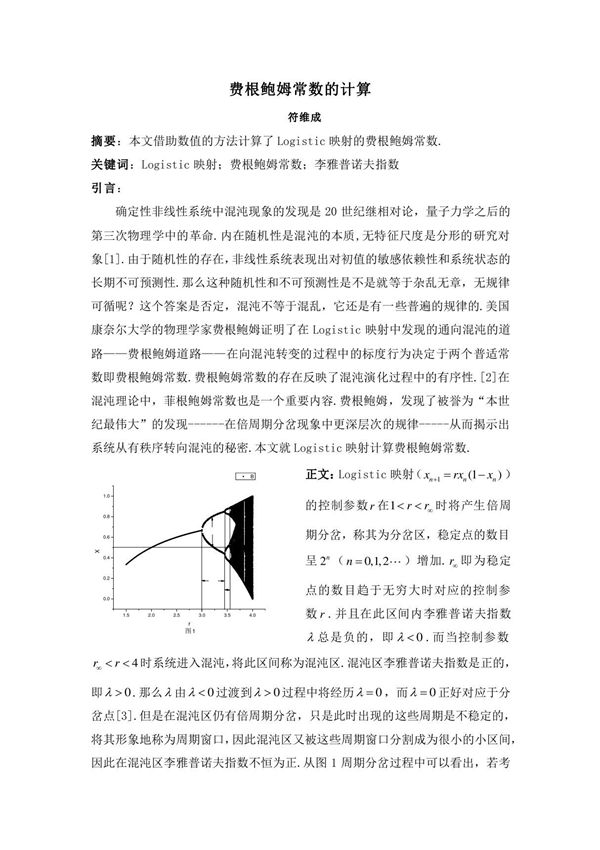
费根鲍姆常数是一类在混沌理论中非常重要的数学常数,主要用于描述非线性动力系统中周期倍增分岔现象的参数收敛行为。它由美国数学家米切尔·费根鲍姆(MitchellFeigenbaum)在20世纪70年代发现,包括两个主要常数:δ(delta)和α(alpha)。费根鲍姆常数δ(约等于4.669201609...)描述了分岔点间距比的收敛值,而α(约等于2.502907875...)描述了分岔时函数尺度缩小的比例。这两个常数在多种非线性系统中具有普适性,意味着它们不仅适用于特定的映射或方程,还广泛出现在不同的混沌系统中。计算费根鲍姆常数通常需要数值方法,例如通过迭代Logistic映射或其他单峰映射来观察分岔行为,并利用极限逼近技术估算δ和α的值。由于这些常数是无理数,计算过程需要高精度的数值分析,通常借助计算机程序(如Python、MATLAB等)来实现。费根鲍姆常数的发现不仅推动了混沌理论的发展,也为理解复杂系统的行为提供了重要的数学工具。