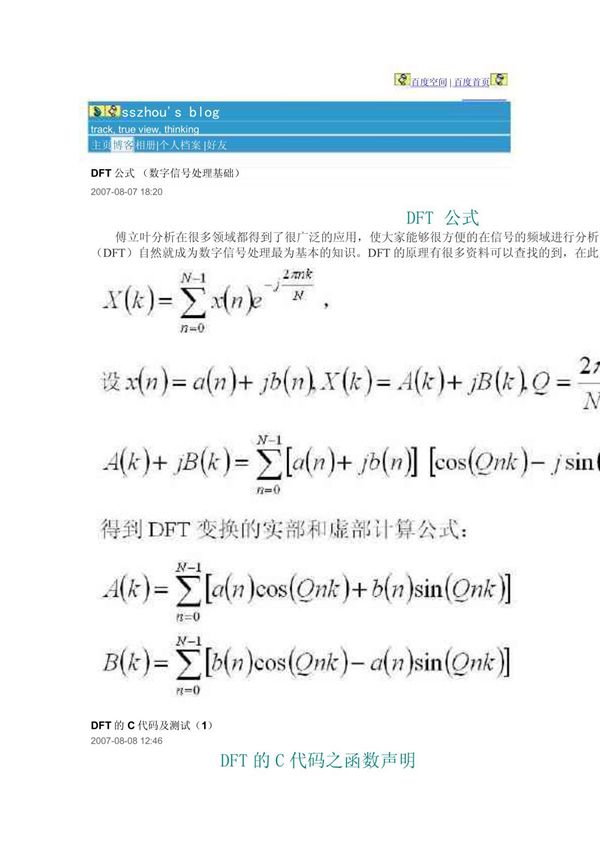
离散傅里叶变换(DiscreteFourierTransform,简称DFT)是数字信号处理中的核心工具之一,用于将离散时间信号从时域转换到频域。它通过对有限长度的离散序列进行频域分析,揭示了信号在不同频率上的能量分布。DFT的数学表达式为:[X[k]=sum_{n=0}^{N-1}x[n]cdote^{-jfrac{2pi}{N}kn}quad(k=0,1,dots,N-1)]其中:-(x[n])是长度为(N)的离散输入序列(时域)-(X[k])是频域的输出序列-(N)为采样点数-(j)表示虚数单位逆离散傅里叶变换(IDFT)的公式为:[x[n]=frac{1}{N}sum_{k=0}^{N-1}X[k]cdote^{jfrac{2pi}{N}kn}quad(n=0,1,dots,N-1)]DFT广泛应用于音频处理、图像分析、通信系统等领域,其快速算法FFT(快速傅里叶变换)大幅降低了计算复杂度,成为实时信号处理的基石。需要注意的是,DFT假设输入信号是周期性的,且分析结果对应的是离散频率点((frac{2pik}{N}))。