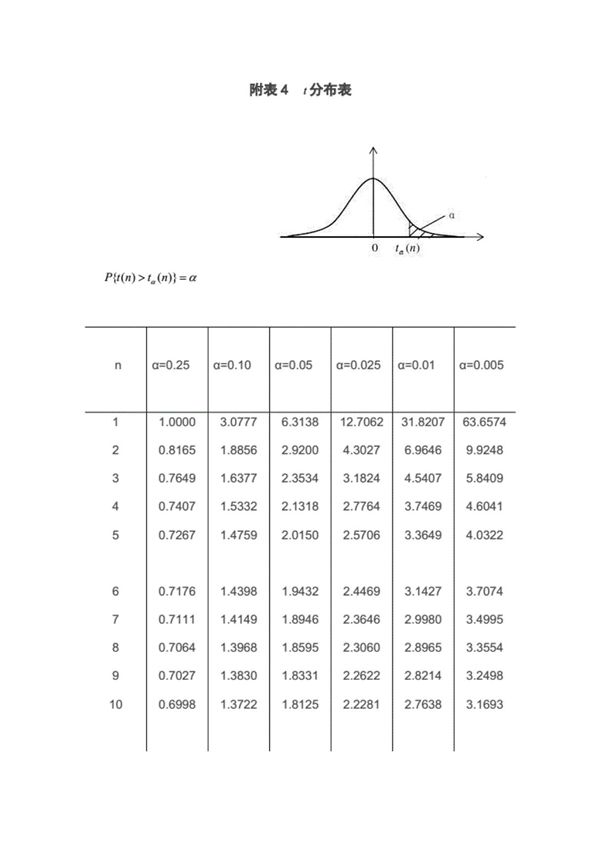
t分布表是统计学中常用的一种参考表格,用于查找t分布在不同自由度和显著性水平下的临界值。t分布由威廉·戈塞特(WilliamGosset)于1908年提出,主要用于小样本情况下估计总体均值的置信区间和进行假设检验。t分布的形状类似于标准正态分布,但随着自由度的减小,其尾部更厚,这意味着在小样本情况下,t分布能更准确地反映数据的变异性。随着自由度增大,t分布逐渐趋近于标准正态分布。t分布表通常包含以下信息:1.自由度(df):表示样本量减一(n-1),影响t分布的形状。2.显著性水平(α):常用的有0.10、0.05、0.01等,表示拒绝原假设的概率阈值。3.单尾或双尾检验:根据研究目的选择对应的临界值。使用t分布表时,需要根据自由度、显著性水平和检验类型(单尾或双尾)查找对应的t值。这个t值用于计算置信区间或与检验统计量比较,以做出统计推断。t分布表在t检验、回归分析等统计方法中有广泛应用,是统计分析中的重要工具之一。