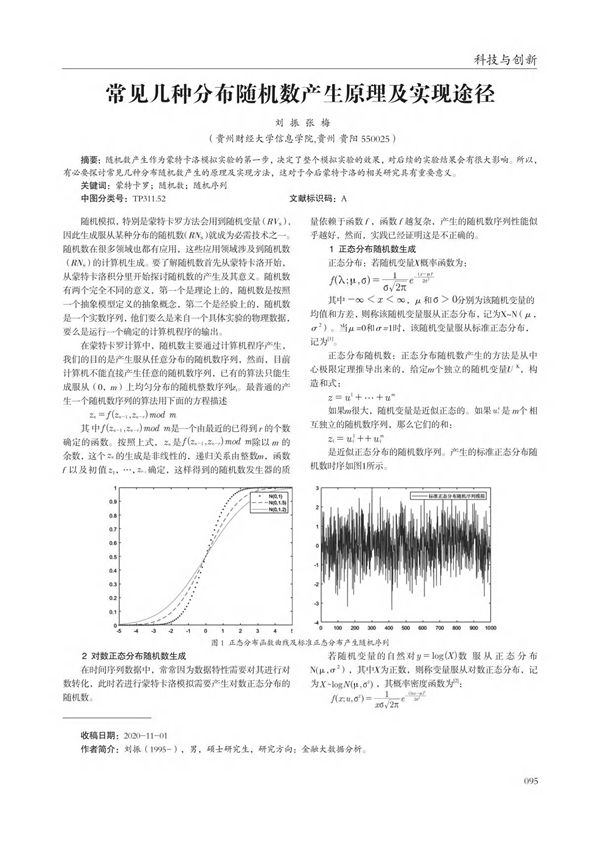
常见几种分布随机数产生原理及实现途径简介在概率统计与计算机模拟中,生成符合特定分布的随机数是一个基础而重要的课题。以下是几种常见分布的随机数生成方法概述:1.均匀分布(UniformDistribution)原理:在指定区间[a,b]内每个数出现的概率相等。实现:通常采用线性同余法等伪随机数生成器产生[0,1]均匀分布,再线性变换到目标区间。2.正态分布(NormalDistribution)原理:基于中心极限定理或变换方法。实现:-Box-Muller变换:将两个均匀分布随机数转换为正态分布-Ziggurat算法:高效的分段拒绝采样法-中心极限定理近似:对多个均匀分布随机数求和3.泊松分布(PoissonDistribution)原理:基于泊松过程与指数分布的关系。实现:-通过指数分布间隔时间累加-Knuth给出的直接生成算法4.指数分布(ExponentialDistribution)原理:利用逆变换法。实现:对均匀分布随机数u,取x=-ln(u)/λ5.二项分布(BinomialDistribution)原理:基于伯努利试验的重复。实现:-多次伯努利试验求和-当n大p小时可用泊松分布近似实现途径:1.编程语言内置函数(如Python的numpy.random)2.自行实现核心算法3.使用专业统计软件(如R语言)4.借助GPU加速的大规模随机数生成库关键考虑因素包括:准确性、效率、可重复性以及特定应用场景的需求。不同的方法在计算复杂度和精度上各有优劣,需要根据具体应用选择合适的方法。