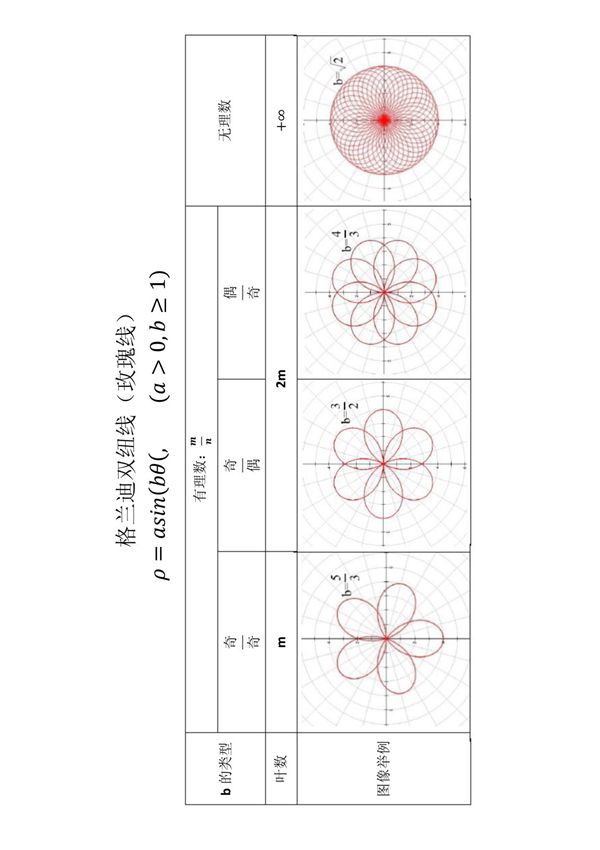
格兰迪双纽线，也称为玫瑰线，是一种极坐标方程描述的优美曲线。其数学表达式通常为r=a*sin(nθ)或r=a*cos(nθ)，其中a控制曲线大小，n决定花瓣数量。当n为奇数时，曲线有n个花瓣；当n为偶数时，有2n个花瓣。这种曲线由意大利数学家GuidoGrandi在18世纪研究，因此得名。玫瑰线在数学、艺术和自然界中都有广泛应用，展现出对称与和谐的几何美感。